이 튜토리얼은 http://clintbellanger.net/articles/isometric_math/의 문서를 번역한것입니다.
아이소메트릭 타일 작업은 평범한 사각형 그리드보다 약간 까다로운 편입니다. 이 튜토리얼은 아이소메트릭 연산을 자신의 머릿속에 집어넣으려는 초보 게임 프로그래머를 위한 것입니다. 저는 단순히 여러분에게 공식을 전달하는 대신, 그것들이 무엇을 하고 어떻게 사용하는지 설명하고자합니다.
아이소메트릭 타일을 다루는 방법은 여러가지가 있지만 여기서는 오직 가장 일반적으로 사용되는 한 방법에 대해 이야기하겠습니다. 이것은 Tiled Map Editor에서 등각 투영을 처리하는 방법이기 때문에 그 툴을 사용할때 정말로 좋은 방법입니다.
직교투영(Orthographic Projection)
아이소메트릭 프로젝트에서 작업 할 때, 여러분의 맵은 여전히 메모리에서 단순한 2차원 배열(이거나 동급)입니다. 여러분이 사이드뷰나 탑뷰와 같이 간단한 직교투영에서 작업하는 것처럼요.
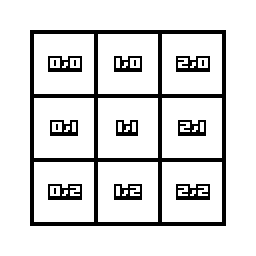
맵 좌표에 있는 격자, 값인 (map.x, map.y)이 메모리에서 어떻게 보이는지 나타납니다.
여러분이 전에 정사각형 그리드로 작업한 적이 있다면 연산은 매우 간단합니다. (등각 투영을 하기전에 먼저 해보시길 추천합니다.) 스크린에 타일을 그리는 것은 단순히 타일의 좌표를 가지고 스크린 위치를 얻을 수 있도록 타일의 크기를 곱하면 됩니다.
screen.x = map.x * TILE_WIDTH;
screen.y = map.y * TILE_HEIGHT;
이 예제에서의 타일은 64x64 픽셀입니다. (2,1) 위치에 있는 타일을 표시하려면 위의 공식을 끼워 넣습니다.
screen.x = 2 * 64; // 128 픽셀과 같음
screen.y = 1 * 64; // 64 픽셀과 같음
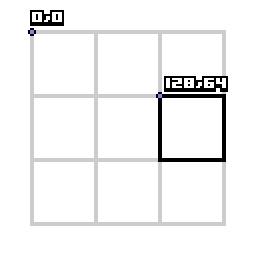
직교 투영 상에서 타일의 화면 위치를 결정하는 것이 보입니다.
등각투영 (Isometric Projection)
다음 그림은 아이소메트릭 뷰에서 화면에 메모리상의 타일을 투사하는 방법을 보여줍니다.
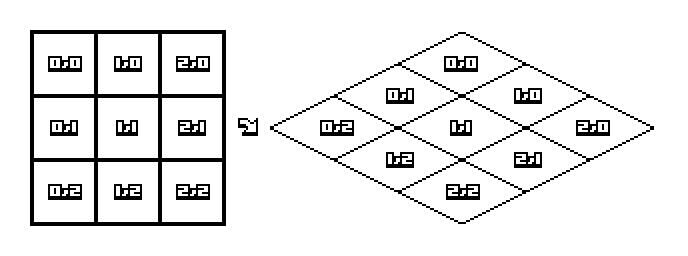
우리는 맵을 위와 같이 구현할겁니다.
이 예제의 아이소메트릭 타일은 128x64 픽셀입니다. 다시 2,1 타일을 그려봅시다. 그러나 지금은 등각 투영으로 그릴겁니다. 우선 2,1 타일이 원점에 비해 어디에 있는지 알아보기 위해 일부 픽셀을 보도록합시다.
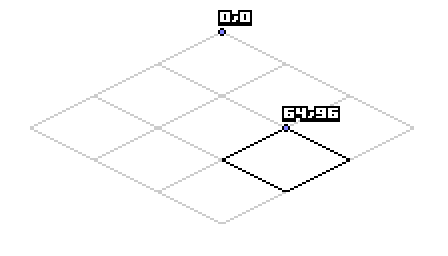
2,1 타일의 위치는 64,96입니다.
여기는 머리가 터지기 쉬운 부분입니다. 회전과 Y스케일을 계산하는 것이 가능하지만 좀더 간단한 방법이 있습니다. 그 트릭은 x와 y를 개별적으로 생각하는 것입니다. 등각투상에 대해서 아래를 잘보세요.
한 타일에서 맵 X축이 +1만큼 증가하면(지도 좌표에서 오른쪽으로 이동) 스크린 X축과 스크린 Y축 모두 증가합니다(스크린 좌표에서 오른쪽과 아래쪽으로 이동). 예제를 보면, 이것이 screen.x를 64(타일 넓이의 반)로, screen.y를 32(타일 높이의 반)로 증가시키는 것을 볼 수 있습니다.
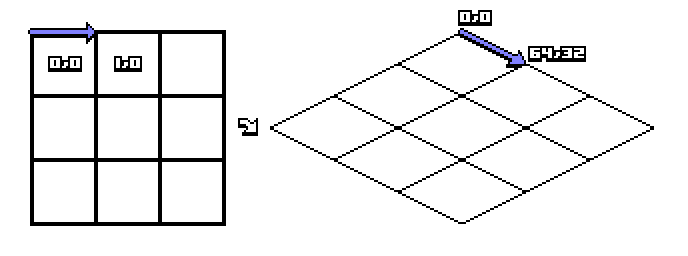
map.x++가 화면 좌표에 +64,+32로 영향을 주는 것을 볼 수 있습니다.
마찬가지로, 맵 Y축이 +1만큼 증가하면(지도 좌표에서 아래로 이동) 스크린 X축이 차감되고 스크린 Y축이 증가합니다(스크린 좌표에서 왼쪽 아래로 이동).
이러한 변경사항을 코드에 다음 형태와 같이 반영합니다.
screen.x = map.x * TILE_WIDTH_HALF - map.y * TILE_WIDTH_HALF;
screen.y = map.x * TILE_HEIGHT_HALF + map.y * TILE_HEIGHT_HALF;
그리고 약간의 간략화를 하면 등각투영의 기본 공식을 얻을 수 있습니다.
screen.x = (map.x - map.y) * TILE_WIDTH_HALF;
screen.y = (map.x + map.y) * TILE_HEIGHT_HALF;
예상된 결과를 얻을 수 있는지 확인하기 위해 2,1타일의 공식을 테스트해봅시다.
screen.x = (2 - 1) * 64; // 64와 같음
screen.y = (2 + 1) * 32; // 96과 같음
스크린 픽셀에서 맵 위치로 다시 산출
이제 정사각형 그리드가 간단히 적용됩니다. 아마 게임의 모든 연산은 정사각형 맵 좌표에서 발생할 것입니다. 뭔가를 그려야할 필요가 있을 경우에만 스크린 픽셀을 산출하겠죠.
가끔 플레이어가 픽셀을 클릭할때 처럼 스크린 픽셀 좌표를 맵 좌표로 변환해야 할 때가 있습니다. 하지만 어떻게 하면 식을 반대로 해서 타일을 찾을 수 있을까요?
지금은 입/출력에서 공식을 알아내는 것 보다는 예전부터 친숙한 대수학을 사용해서 함수를 뒤집도록 하겠습니다.
// 기본적인 아이소메트릭 맵에서 스크린 좌표로 변환하는 것은 다음과 같습니다. screen.x = (map.x - map.y) * TILE_WIDTH_HALF; screen.y = (map.x + map.y) * TILE_HEIGHT_HALF; //map.x에 대한 첫 번째방정식을 풉니다.screen.x == (map.x - map.y) * TILE_WIDTH_HALF screen.x / TILE_WIDTH_HALF == map.x - map.y map.x == screen.x / TILE_WIDTH_HALF + map.y //map.y에 대한 두 번째방정식을 풉니다.screen.y == (map.x + map.y) * TILE_HEIGHT_HALF screen.y / TILE_HEIGHT_HALF == map.x + map.y map.y == screen.y / TILE_HEIGHT_HALF - map.x //첫 번째 방정식의 'map.y'를 두 번째 방정식과 같도록 치환합니다. map.x == screen.x / TILE_WIDTH_HALF + map.y map.x == screen.x / TILE_WIDTH_HALF + screen.y / TILE_HEIGHT_HALF - map.x 2(map.x) == screen.x / TILE_WIDTH_HALF + screen.y / TILE_HEIGHT_HALF map.x == (screen.x / TILE_WIDTH_HALF + screen.y / TILE_HEIGHT_HALF) /2 // 그리고 map.y에 대해 같은 작업을 수행합니다. map.y == screen.y / TILE_HEIGHT_HALF - (screen.x / TILE_WIDTH_HALF + map.y) map.y == screen.y / TILE_HEIGHT_HALF -(screen.x / TILE_WIDTH_HALF) - map.y 2(map.y) == screen.y / TILE_HEIGHT_HALF -(screen.x / TILE_WIDTH_HALF) map.y == (screen.y / TILE_HEIGHT_HALF -(screen.x / TILE_WIDTH_HALF)) /2 //그래서 최종 실제 명령은 다음과 같습니다.map.x = (screen.x / TILE_WIDTH_HALF + screen.y / TILE_HEIGHT_HALF) /2; map.y = (screen.y / TILE_HEIGHT_HALF -(screen.x / TILE_WIDTH_HALF)) /2;

도전과제 해제!
졸업후 사용된 대수학
지정된 스크린 픽셀 좌표는 64,94 이며, (2,1)타일로 재산출될것 같네요.
map.x = (screen.x / TILE_WIDTH_HALF + screen.y / TILE_HEIGHT_HALF) /2;
map.x = (64 / 64 + 96 / 32) /2;
map.x = (1 + 3) /2;
map.x = 2;
map.y = (screen.y / TILE_HEIGHT_HALF -(screen.x / TILE_WIDTH_HALF)) /2;
map.y = (96 / 32 - (64 / 64)) /2;
map.y = (3 - 1) /2;
map.y = 1;

수학적!
주의
아이소메트릭의 원점은 상단 모서리인것을 알 수 있습니다. 우리가 보통 스프라이트를 그릴 때에는 왼쪽 상단 모서리에서 부터 그립니다. 그리기 전에 타일의 크기에 따라 조정할 수 있습니다. 일반 크기 타일의 예: screen.x -= TILE_WIDTH_HALF;
이 공식은 또한 카메라를 고려하지 않습니다. 기본적으로 카메라는 그냥 직교 투영 게임에서와 같이 오프셋을 그립니다. 투영된 맵의 중앙은 X축 0이기 때문에 카메라 오프셋을 가진듯이 화면의 중앙에 하길원한다면 screen.x += SCREEN_WIDTH_HALF;를 참고하세요.
이 공식은 서브 타일 위치에도 적용됩니다. 모두 부동소수점으로 처리했다면 맵 위치 (2.5, 1.5)는 스크린 위치(64.0, 128.0)이 되고 그 반대도 마찬가지입니다.
어쨋든 부동소수점을 사용할것이라면 screen_to_map함수를 약간 단순화 할 수 있습니다. (왜냐하면 정수 나눗셈과 상관 없기 때문이죠)
// 부동 소숫점 나눗셈을 하는 경우에만
// 상수를 둘로 나누는 것을 고려합니다.
map.x = screen.x / TILE_WIDTH + screen.y / TILE_HEIGHT;
map.y = screen.y / TILE_HEIGHT - screen.x / TILE_WIDTH;
저는 스크린과 맵 좌표의 빠른 전환을 위해 두 개의 유틸리티 기능을 설정할 것을 제안합니다. 맵 좌표의 실제 계산은 모두 하도록 하고, 스크린 좌표는 입력(클릭/터치) 및 출력(렌더링)에서 산출되게 하십시오.
번역에 도움주신 분들
구글 번역기, 쇼타베르토, 예리나래, 王코털
오역 및 미번역 부분은 올바른 번역을 제시해 주시기 바랍니다.





번한하시느라 수고하셨습니다'ㅅ'/